Core Functions in Depth

If you’re a huge fan of the angsty, teenager-centric, quasi–soap opera The Vampire Diaries like I am, you’ll remember the episode where the lead protagonist, Elena, starts to question her pale, mysterious crush’s behavior: “Why did he instantly vanish without a trace when I scraped my knee?” and “How come his face turned into a grotesque mask of death when I nicked my finger?” and so on.

You might be asking yourself similar questions if you’ve started playing with Clojure’s core functions. “Why did map return a list when I gave it a vector?” and “How come reduce treats my map like a list of vectors?” and so on. (With Clojure, though, you’re at least spared from contemplating the profound existential horror of being a 17-year-old for eternity.)

In this chapter, you’ll learn about Clojure’s deep, dark, bloodthirsty, supernatur—*cough* I mean, in this chapter, you’ll learn about Clojure’s underlying concept of programming to abstractions and about the sequence and collection abstractions. You’ll also learn about lazy sequences. This will give you the grounding you need to read the documentation for functions you haven’t used before and to understand what’s happening when you give them a try.

Next, you’ll get more experience with the functions you’ll be reaching for the most. You’ll learn how to work with lists, vectors, maps, and sets with the functions map, reduce, into, conj, concat, some, filter, take, drop, sort, sort-by, and identity. You’ll also learn how to create new functions with apply, partial, and complement. All this information will help you understand how to do things the Clojure way, and it will give you a solid foundation for writing your own code as well as for reading and learning from others’ projects.

Finally, you’ll learn how to parse and query a CSV of vampire data to determine what nosferatu lurk in your hometown.

Programming to Abstractions

To understand programming to abstractions, let’s compare Clojure to a language that wasn’t built with that principle in mind: Emacs Lisp (elisp). In elisp, you can use the mapcar function to derive a new list, which is similar to how you use map in Clojure. However, if you want to map over a hash map (similar to Clojure’s map data structure) in elisp, you’ll need to use the maphash function, whereas in Clojure you can still just use map. In other words, elisp uses two different, data structure–specific functions to implement the map operation, but Clojure uses only one. You can also call reduce on a map in Clojure, whereas elisp doesn’t provide a function for reducing a hash map.

The reason is that Clojure defines map and reduce functions in terms of the sequence abstraction, not in terms of specific data structures. As long as a data structure responds to the core sequence operations (the functions first, rest, and cons, which we’ll look at more closely in a moment), it will work with map, reduce, and oodles of other sequence functions for free. This is what Clojurists mean by programming to abstractions, and it’s a central tenet of Clojure philosophy.

I think of abstractions as named collections of operations. If you can perform all of an abstraction’s operations on an object, then that object is an instance of the abstraction. I think this way even outside of programming. For example, the battery abstraction includes the operation “connect a conducting medium to its anode and cathode,” and the operation’s output is electrical current. It doesn’t matter if the battery is made out of lithium or out of potatoes. It’s a battery as long as it responds to the set of operations that define battery.

Similarly, map doesn’t care about how lists, vectors, sets, and maps are implemented. It only cares about whether it can perform sequence operations on them. Let’s look at how map is defined in terms of the sequence abstraction so you can understand programming to abstractions in general.

Treating Lists, Vectors, Sets, and Maps as Sequences

If you think about the map operation independently of any programming language, or even of programming altogether, its essential behavior is to derive a new sequence y from an existing sequence x using a function ƒ such that y1 = ƒ(x1), y2 = ƒ(x2), . . . yn = ƒ(xn). Figure 4-1 illustrates how you might visualize a mapping applied to a sequence.

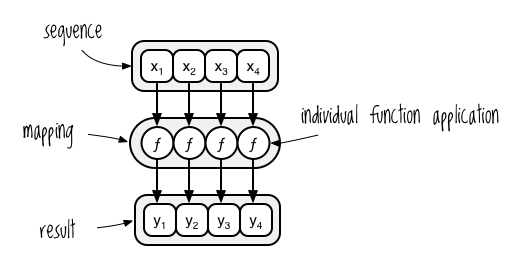
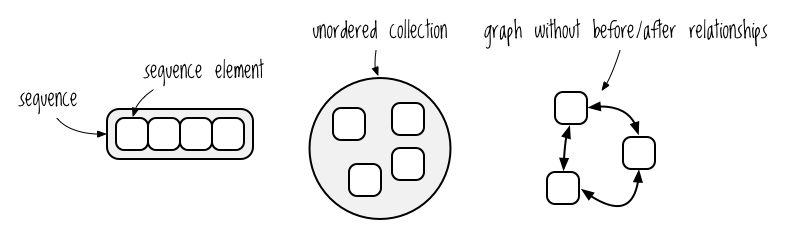
The term sequence here refers to a collection of elements organized in linear order, as opposed to, say, an unordered collection or a graph without a before-and-after relationship between its nodes. Figure 4-2 shows how you might visualize a sequence, in contrast to the other two collections mentioned.

Absent from this description of mapping and sequences is any mention of lists, vectors, or other concrete data structures. Clojure is designed to allow us to think and program in such abstract terms as much as possible, and it does this by implementing functions in terms of data structure abstractions. In this case, map is defined in terms of the sequence abstraction. In conversation, you would say map, reduce, and other sequence functions take a sequence or even take a seq. In fact, Clojurists usually use seq instead of sequence, using terms like seq functions and the seq library to refer to functions that perform sequential operations. Whether you use sequence or seq, you’re indicating that the data structure in question will be treated as a sequence and that what it actually is in its truest heart of hearts doesn’t matter in this context.

If the core sequence functions first, rest, and cons work on a data structure, you can say the data structure implements the sequence abstraction. Lists, vectors, sets, and maps all implement the sequence abstraction, so they all work with map, as shown here:

(defn titleize
  [topic]
  (str topic " for the Brave and True"))

(map titleize ["Hamsters" "Ragnarok"])
; => ("Hamsters for the Brave and True" "Ragnarok for the Brave and True")

(map titleize '("Empathy" "Decorating"))
; => ("Empathy for the Brave and True" "Decorating for the Brave and True")

(map titleize #{"Elbows" "Soap Carving"})
; => ("Elbows for the Brave and True" "Soap Carving for the Brave and True")

(map #(titleize (second %)) {:uncomfortable-thing "Winking"})
; => ("Winking for the Brave and True")

The first two examples show that map works identically with vectors and lists. The third example shows that map can work with unsorted sets. In the fourth example, you must call second on the anonymous function’s argument before title-izing it because the argument is a map. I’ll explain why soon, but first let’s look at the three functions that define the sequence abstraction.

first, rest, and cons

In this section, we’ll take a quick detour into JavaScript to implement a linked list and three core functions: first, rest, and cons. After those three core functions are implemented, I’ll show how you to build map with them.

The point is to appreciate the distinction between the seq abstraction in Clojure and the concrete implementation of a linked list. It doesn’t matter how a particular data structure is implemented: when it comes to using seq functions on a data structure, all Clojure asks is “can I first, rest, and cons it?” If the answer is yes, you can use the seq library with that data structure.

In a linked list, nodes are linked in a linear sequence. Here’s how you might create one in JavaScript. In this snippet, next is null because this is the last node in the list:

var node3 = {
  value: "last",
  next: null
};

In this snippet, node2’s next points to node3, and node1’s next points to node2; that’s the “link” in “linked list”:

var node2 = {
  value: "middle",
  next: node3
};

var node1 = {
  value: "first",
  next: node2
};

Graphically, you could represent this list as shown in Figure 4-3.

You can perform three core functions on a linked list: first, rest, and cons. first returns the value for the requested node, rest returns the remaining values after the requested node, and cons adds a new node with the given value to the beginning of the list. After those are implemented, you can implement map, reduce, filter, and other seq functions on top of them.

The following code shows how we would implement and use first, rest, and cons with our JavaScript node example, as well as how to use them to return specific nodes and derive a new list. Note that the parameter of first and rest is named node. This might be confusing because you might say, “Ain’t I getting the first element of a list?” Well, you operate on the elements of a list one node at a time!

var first = function(node) {
  return node.value;
};

var rest = function(node) {
  return node.next;
};

var cons = function(newValue, node) {
  return {
    value: newValue,
    next: node
  };
};

first(node1);
// => "first"

first(rest(node1));
// => "middle"

first(rest(rest(node1)));
// => "last"

var node0 = cons("new first", node1);
first(node0);
// => "new first"

first(rest(node0));
// => "first"

As noted previously, you can implement map in terms of first, rest, and cons:

var map = function (list, transform) {
  if (list === null) {
    return null;
  } else {
    return cons(transform(first(list)), map(rest(list), transform));
  }
}

This function transforms the first element of the list and then calls itself again on the rest of the list until it reaches the end (a null). Let’s see it in action! In this example, you’re mapping the list that begins with node1, returning a new list where the string " mapped!" is appended to each node’s value. Then you’re using first to return the first node’s value:

first(
  map(node1, function (val) { return val + " mapped!"})
);

// => "first mapped!"

So here’s the cool thing: because map is implemented completely in terms of cons, first, and rest, you could actually pass it any data structure and it would work as long as cons, first, and rest work on that data structure.

Here’s how they might work for an array:

var first = function (array) {
  return array[0];
}

var rest = function (array) {
  var sliced = array.slice(1, array.length);
  if (sliced.length == 0) {
    return null;
  } else {
    return sliced;
  }
}

var cons = function (newValue, array) {
  return [newValue].concat(array);
}


var list = ["Transylvania", "Forks, WA"];
map(list, function (val) { return val + " mapped!"})
// => ["Transylvania mapped!", "Forks, WA mapped!"]

This code snippet defines first, rest, and cons in terms of JavaScript’s array functions. Meanwhile, map continues referencing functions named first, rest, and cons, so now it works on array. So, if you can just implement first, rest, and cons, you get map for free along with the aforementioned oodles of other functions.

Abstraction Through Indirection

At this point, you might object that I’m just kicking the can down the road because we’re still left with the problem of how a function like first is able to work with different data structures. Clojure does this using two forms of indirection. In programming, indirection is a generic term for the mechanisms a language employs so that one name can have multiple, related meanings. In this case, the name first has multiple, data structure–specific meanings. Indirection is what makes abstraction possible.

Polymorphism is one way that Clojure provides indirection. I don’t want to get lost in the details, but basically, polymorphic functions dispatch to different function bodies based on the type of the argument supplied. (It’s not so different from how multiple-arity functions dispatch to different function bodies based on the number of arguments you provide.)

Note Clojure has two constructs for defining polymorphic dispatch: the host platform’s interface construct and platform-independent protocols. But it’s not necessary to understand how these work when you’re just getting started. I’ll cover protocols in Chapter 13.

When it comes to sequences, Clojure also creates indirection by doing a kind of lightweight type conversion, producing a data structure that works with an abstraction’s functions. Whenever Clojure expects a sequence—for example, when you call map, first, rest, or cons—it calls the seq function on the data structure in question to obtain a data structure that allows for first, rest, and cons:

(seq '(1 2 3))
; => (1 2 3)

(seq [1 2 3])
; => (1 2 3)

(seq #{1 2 3})
; => (1 2 3)

(seq {:name "Bill Compton" :occupation "Dead mopey guy"})
; => ([:name "Bill Compton"] [:occupation "Dead mopey guy"])

There are two notable details here. First, seq always returns a value that looks and behaves like a list; you’d call this value a sequence or seq. Second, the seq of a map consists of two-element key-value vectors. That’s why map treats your maps like lists of vectors! You can see this in the "Bill Compton" example. I wanted to point out this example in particular because it might be surprising and confusing. It was for me when I first started using Clojure. Knowing these underlying mechanisms will spare you from the kind of frustration and general mopiness often exhibited by male vampires trying to retain their humanity.

You can convert the seq back into a map by using into to stick the result into an empty map (you’ll look at into closely later):

(into {} (seq {:a 1 :b 2 :c 3}))
; => {:a 1, :c 3, :b 2}

So, Clojure’s sequence functions use seq on their arguments. The sequence functions are defined in terms of the sequence abstraction, using first, rest, and cons. As long as a data structure implements the sequence abstraction, it can use the extensive seq library, which includes such superstar functions as reduce, filter, distinct, group-by, and dozens more.

The takeaway here is that it’s powerful to focus on what we can do with a data structure and to ignore, as much as possible, its implementation. Implementations rarely matter in and of themselves. They’re just a means to an end. In general, programming to abstractions gives you power by letting you use libraries of functions on different data structure regardless of how those data structures are implemented.

Seq Function Examples

Clojure’s seq library is full of useful functions that you’ll use all the time. Now that you have a deeper understanding of Clojure’s sequence abstraction, let’s look at these functions in detail. If you’re new to Lisp and functional programming, these examples will be surprising and delightful.

map

You’ve seen many examples of map by now, but this section shows map doing two new tasks: taking multiple collections as arguments and taking a collection of functions as an argument. It also highlights a common map pattern: using keywords as the mapping function.

So far, you’ve only seen examples of map operating on one collection. In the following code, the collection is the vector [1 2 3]:

(map inc [1 2 3])
; => (2 3 4)

However, you can also give map multiple collections. Here’s a simple example to show how this works:

(map str ["a" "b" "c"] ["A" "B" "C"])
; => ("aA" "bB" "cC")

It’s as if map does the following:

(list (str "a" "A") (str "b" "B") (str "c" "C"))

When you pass map multiple collections, the elements of the first collection (["a" "b" "c"]) will be passed as the first argument of the mapping function (str), the elements of the second collection (["A" "B" "C"]) will be passed as the second argument, and so on. Just be sure that your mapping function can take a number of arguments equal to the number of collections you’re passing to map.

The following example shows how you could use this capability if you were a vampire trying to curb your human consumption. You have two vectors, one representing human intake in liters and another representing critter intake for the past four days. The unify-diet-data function takes a single day’s data for both human and critter feeding and unifies the two into a single map:

(def human-consumption   [8.1 7.3 6.6 5.0])
(def critter-consumption [0.0 0.2 0.3 1.1])
(defn unify-diet-data
  [human critter]
  {:human human
   :critter critter})

(map unify-diet-data human-consumption critter-consumption)
; => ({:human 8.1, :critter 0.0}
      {:human 7.3, :critter 0.2}
      {:human 6.6, :critter 0.3}
      {:human 5.0, :critter 1.1})

Good job laying off the human!

Another fun thing you can do with map is pass it a collection of functions. You could use this if you wanted to perform a set of calculations on different collections of numbers, like so:

(def sum #(reduce + %))
(def avg #(/ (sum %) (count %)))
(defn stats
  [numbers]
  (map #(% numbers) [sum count avg]))

(stats [3 4 10])
; => (17 3 17/3)

(stats [80 1 44 13 6])
; => (144 5 144/5)

In this example, the stats function iterates over a vector of functions, applying each function to numbers.

Additionally, Clojurists often use map to retrieve the value associated with a keyword from a collection of map data structures. Because keywords can be used as functions, you can do this succinctly. Here’s an example:

(def identities
  [{:alias "Batman" :real "Bruce Wayne"}
   {:alias "Spider-Man" :real "Peter Parker"}
   {:alias "Santa" :real "Your mom"}
   {:alias "Easter Bunny" :real "Your dad"}])

(map :real identities)
; => ("Bruce Wayne" "Peter Parker" "Your mom" "Your dad")

(If you are five, then I apologize profusely.)

reduce

Chapter 3 showed how reduce processes each element in a sequence to build a result. This section shows a couple of other ways to use it that might not be obvious.

The first use is to transform a map’s values, producing a new map with the same keys but with updated values:

(reduce (fn [new-map [key val]]
          (assoc new-map key (inc val)))
        {}
        {:max 30 :min 10})
; => {:max 31, :min 11}

In this example, reduce treats the argument {:max 30 :min 10} as a sequence of vectors, like ([:max 30] [:min 10]). Then, it starts with an empty map (the second argument) and builds it up using the first argument, an anonymous function. It’s as if reduce does this:

(assoc (assoc {} :max (inc 30))
       :min (inc 10))

The function assoc takes three arguments: a map, a key, and a value. It derives a new map from the map you give it by associating the given key with the given value. For example, (assoc {:a 1} :b 2) would return {:a 1 :b 2}

Another use for reduce is to filter out keys from a map based on their value. In the following example, the anonymous function checks whether the value of a key-value pair is greather than 4. If it isn’t, then the key-value pair is filtered out. In the map {:human 4.1 :critter 3.9}, 3.9 is less than 4, so the :critter key and its 3.9 value are filtered out.

(reduce (fn [new-map [key val]]
          (if (> val 4)
            (assoc new-map key val)
            new-map))
        {}
        {:human 4.1
         :critter 3.9})
; => {:human 4.1}

The takeaway here is that reduce is a more flexible function than it first appears. Whenever you want to derive a new value from a seqable data structure, reduce will usually be able to do what you need. If you want an exercise that will really blow your hair back, try implementing map using reduce, and then do the same for filter and some after you read about them later in this chapter.

take, drop, take-while, and drop-while

take and drop both take two arguments: a number and a sequence. take returns the first n elements of the sequence, whereas drop returns the sequence with the first n elements removed:

(take 3 [1 2 3 4 5 6 7 8 9 10])
; => (1 2 3)

(drop 3 [1 2 3 4 5 6 7 8 9 10])
; => (4 5 6 7 8 9 10)

Their cousins take-while and drop-while are a bit more interesting. Each takes a predicate function (a function whose return value is evaluated for truth or falsity) to determine when it should stop taking or dropping. Suppose, for example, that you had a vector representing entries in your “food” journal. Each entry has the month and day, along with what you ate. To preserve space, we’ll only include a few entries:

(def food-journal
  [{:month 1 :day 1 :human 5.3 :critter 2.3}
   {:month 1 :day 2 :human 5.1 :critter 2.0}
   {:month 2 :day 1 :human 4.9 :critter 2.1}
   {:month 2 :day 2 :human 5.0 :critter 2.5}
   {:month 3 :day 1 :human 4.2 :critter 3.3}
   {:month 3 :day 2 :human 4.0 :critter 3.8}
   {:month 4 :day 1 :human 3.7 :critter 3.9}
   {:month 4 :day 2 :human 3.7 :critter 3.6}])

With take-while, you can retrieve just January’s and February’s data. take-while traverses the given sequence (in this case, food-journal), applying the predicate function to each element.

This example uses the anonymous function #(< (:month %) 3) to test whether the journal entry’s month is out of range:

(take-while #(< (:month %) 3) food-journal)
; => ({:month 1 :day 1 :human 5.3 :critter 2.3}
      {:month 1 :day 2 :human 5.1 :critter 2.0}
      {:month 2 :day 1 :human 4.9 :critter 2.1}
      {:month 2 :day 2 :human 5.0 :critter 2.5})

When take-while reaches the first March entry, the anonymous function returns false, and take-while returns a sequence of every element it tested until that point.

The same idea applies with drop-while except that it keeps dropping elements until one tests true:

(drop-while #(< (:month %) 3) food-journal)
; => ({:month 3 :day 1 :human 4.2 :critter 3.3}
      {:month 3 :day 2 :human 4.0 :critter 3.8}
      {:month 4 :day 1 :human 3.7 :critter 3.9}
      {:month 4 :day 2 :human 3.7 :critter 3.6})

By using take-while and drop-while together, you can get data for just February and March:

(take-while #(< (:month %) 4)
            (drop-while #(< (:month %) 2) food-journal))
; => ({:month 2 :day 1 :human 4.9 :critter 2.1}
      {:month 2 :day 2 :human 5.0 :critter 2.5}
      {:month 3 :day 1 :human 4.2 :critter 3.3}
      {:month 3 :day 2 :human 4.0 :critter 3.8})

This example uses drop-while to get rid of the January entries, and then it uses take-while on the result to keep taking entries until it reaches the first April entry.

filter and some

Use filter to return all elements of a sequence that test true for a predicate function. Here are the journal entries where human consumption is less than five liters:

(filter #(< (:human %) 5) food-journal)
; => ({:month 2 :day 1 :human 4.9 :critter 2.1}
      {:month 3 :day 1 :human 4.2 :critter 3.3}
      {:month 3 :day 2 :human 4.0 :critter 3.8}
      {:month 4 :day 1 :human 3.7 :critter 3.9}
      {:month 4 :day 2 :human 3.7 :critter 3.6})

You might be wondering why we didn’t just use filter in the take-while and drop-while examples earlier. Indeed, filter would work for that too. Here we’re grabbing the January and February data, just like in the take-while example:

(filter #(< (:month %) 3) food-journal)
; => ({:month 1 :day 1 :human 5.3 :critter 2.3}
      {:month 1 :day 2 :human 5.1 :critter 2.0}
      {:month 2 :day 1 :human 4.9 :critter 2.1}
      {:month 2 :day 2 :human 5.0 :critter 2.5})

This use is perfectly fine, but filter can end up processing all of your data, which isn’t always necessary. Because the food journal is already sorted by date, we know that take-while will return the data we want without having to examine any of the data we won’t need. Therefore, take-while can be more efficient.

Often, you want to know whether a collection contains any values that test true for a predicate function. The some function does that, returning the first truthy value (any value that’s not false or nil) returned by a predicate function:

(some #(> (:critter %) 5) food-journal)
; => nil

(some #(> (:critter %) 3) food-journal)
; => true

You don’t have any food journal entries where you consumed more than five liters from critter sources, but you do have at least one where you consumed more than three liters. Notice that the return value in the second example is true and not the actual entry that produced the true value. The reason is that the anonymous function #(> (:critter %) 3) returns true or false. Here’s how you could return the entry:

(some #(and (> (:critter %) 3) %) food-journal)
; => {:month 3 :day 1 :human 4.2 :critter 3.3}

Here, a slightly different anonymous function uses and to first check whether the condition (> (:critter %) 3) is true, and then returns the entry when the condition is indeed true.

sort and sort-by

You can sort elements in ascending order with sort:

(sort [3 1 2])
; => (1 2 3)

If your sorting needs are more complicated, you can use sort-by, which allows you to apply a function (sometimes called a key function) to the elements of a sequence and use the values it returns to determine the sort order. In the following example, which is taken from http://clojuredocs.org/, count is the key function:

(sort-by count ["aaa" "c" "bb"])
; => ("c" "bb" "aaa")

If you were sorting using sort, the elements would be sorted in alphabetical order, returning ("aaa" "bb" "c"). Instead, the result is ("c" "bb" "aaa") because you’re sorting by count and the count of "c" is 1, "bb" is 2, and "aaa" is 3.

concat

Finally, concat simply appends the members of one sequence to the end of another:

(concat [1 2] [3 4])
; => (1 2 3 4)

Lazy Seqs

As you saw earlier, map first calls seq on the collection you pass to it. But that’s not the whole story. Many functions, including map and filter, return a lazy seq. A lazy seq is a seq whose members aren’t computed until you try to access them. Computing a seq’s members is called realizing the seq. Deferring the computation until the moment it’s needed makes your programs more efficient, and it has the surprising benefit of allowing you to construct infinite sequences.

Demonstrating Lazy Seq Efficiency

To see lazy seqs in action, pretend that you’re part of a modern-day task force whose purpose is to identify vampires. Your intelligence agents tell you that there is only one active vampire in your city, and they’ve helpfully narrowed down the list of suspects to a million people. Your boss gives you a list of one million Social Security numbers and shouts, “Get it done, McFishwich!”

Thankfully, you are in possession of a Vampmatic 3000 computifier, the state-of-the-art device for vampire identification. Because the source code for this vampire-hunting technology is proprietary, I’ve stubbed it out to simulate the time it would take to perform this task. Here is a subset of a vampire database:

(def vampire-database
  {0 {:makes-blood-puns? false, :has-pulse? true  :name "McFishwich"}
   1 {:makes-blood-puns? false, :has-pulse? true  :name "McMackson"}
   2 {:makes-blood-puns? true,  :has-pulse? false :name "Damon Salvatore"}
   3 {:makes-blood-puns? true,  :has-pulse? true  :name "Mickey Mouse"}})

(defn vampire-related-details
  [social-security-number]
  (Thread/sleep 1000)
  (get vampire-database social-security-number))

(defn vampire?
  [record]
  (and (:makes-blood-puns? record)
       (not (:has-pulse? record))
       record))

(defn identify-vampire
  [social-security-numbers]
  (first (filter vampire?
                 (map vampire-related-details social-security-numbers))))

You have a function, vampire-related-details, which takes one second to look up an entry from the database. Next, you have a function, vampire?, which returns a record if it passes the vampire test; otherwise, it returns false. Finally, identify-vampire maps Social Security numbers to database records and then returns the first record that indicates vampirism.

To show how much time it takes to run these functions, you can use the time operation. When you use time, your code behaves exactly as it would if you didn’t use time, but with one exception: a report of the elapsed time is printed. Here’s an example:

(time (vampire-related-details 0))
; => "Elapsed time: 1001.042 msecs"
; => {:name "McFishwich", :makes-blood-puns? false, :has-pulse? true}

The first printed line reports the time taken by the given operation—in this case, 1,001.042 milliseconds. The second is the return value, which is your database record in this case. The return value is exactly the same as it would have been if you hadn’t used time.

A nonlazy implementation of map would first have to apply vampire-related-details to every member of social-security-numbers before passing the result to filter. Because you have one million suspects, this would take one million seconds, or 12 days, and half your city would be dead by then! Of course, if it turns out that the only vampire is the last suspect in the record, it will still take that much time with the lazy version, but at least there’s a good chance that it won’t.

Because map is lazy, it doesn’t actually apply vampire-related-details to Social Security numbers until you try to access the mapped element. In fact, map returns a value almost instantly:

(time (def mapped-details (map vampire-related-details (range 0 1000000))))
; => "Elapsed time: 0.049 msecs"
; => #'user/mapped-details

In this example, range returns a lazy sequence consisting of the integers from 0 to 999,999. Then, map returns a lazy sequence that is associated with the name mapped-details. Because map didn’t actually apply vampire-related-details to any of the elements returned by range, the entire operation took barely any time—certainly less than 12 days.

You can think of a lazy seq as consisting of two parts: a recipe for how to realize the elements of a sequence and the elements that have been realized so far. When you use map, the lazy seq it returns doesn’t include any realized elements yet, but it does have the recipe for generating its elements. Every time you try to access an unrealized element, the lazy seq will use its recipe to generate the requested element.

In the previous example, mapped-details is unrealized. Once you try to access a member of mapped-details, it will use its recipe to generate the element you’ve requested, and you’ll incur the one-second-per-database-lookup cost:

(time (first mapped-details))
; => "Elapsed time: 32030.767 msecs"
; => {:name "McFishwich", :makes-blood-puns? false, :has-pulse? true}

This operation took about 32 seconds. That’s much better than one million seconds, but it’s still 31 seconds more than we would have expected. After all, you’re only trying to access the very first element, so it should have taken only one second.

The reason it took 32 seconds is that Clojure chunks its lazy sequences, which just means that whenever Clojure has to realize an element, it preemptively realizes some of the next elements as well. In this example, you wanted only the very first element of mapped-details, but Clojure went ahead and prepared the next 31 as well. Clojure does this because it almost always results in better performance.

Thankfully, lazy seq elements need to be realized only once. Accessing the first element of mapped-details again takes almost no time:

(time (first mapped-details))
; => "Elapsed time: 0.022 msecs"
; => {:name "McFishwich", :makes-blood-puns? false, :has-pulse? true}

With all this newfound knowledge, you can efficiently mine the vampire database to find the fanged culprit:

(time (identify-vampire (range 0 1000000)))
"Elapsed time: 32019.912 msecs"
; => {:name "Damon Salvatore", :makes-blood-puns? true, :has-pulse? false}

Ooh! That’s why Damon makes those creepy puns!

Infinite Sequences

One cool, useful capability that lazy seqs give you is the ability to construct infinite sequences. So far, you’ve only worked with lazy sequences generated from vectors or lists that terminated. However, Clojure comes with a few functions to create infinite sequences. One easy way to create an infinite sequence is with repeat, which creates a sequence whose every member is the argument you pass:

(concat (take 8 (repeat "na")) ["Batman!"])
; => ("na" "na" "na" "na" "na" "na" "na" "na" "Batman!")

In this case, you create an infinite sequence whose every element is the string "na", then use that to construct a sequence that may or not provoke nostalgia.

You can also use repeatedly, which will call the provided function to generate each element in the sequence:

(take 3 (repeatedly (fn [] (rand-int 10))))
; => (1 4 0)

Here, the lazy sequence returned by repeatedly generates every new element by calling the anonymous function (fn [] (rand-int 10)), which returns a random integer between 0 and 9. If you run this in your REPL, your result will most likely be different from this one.

A lazy seq’s recipe doesn’t have to specify an endpoint. Functions like first and take, which realize the lazy seq, have no way of knowing what will come next in a seq, and if the seq keeps providing elements, well, they’ll just keep taking them. You can see this if you construct your own infinite sequence:

(defn even-numbers
  ([] (even-numbers 0))
  ([n] (cons n (lazy-seq (even-numbers (+ n 2))))))

(take 10 (even-numbers))
; => (0 2 4 6 8 10 12 14 16 18)

This example is a bit mind-bending because of its use of recursion. It helps to remember that cons returns a new list with an element appended to the given list:

(cons 0 '(2 4 6))
; => (0 2 4 6)

(Incidentally, Lisp programmers call it consing when they use the cons function.)

In even-numbers, you’re consing to a lazy list, which includes a recipe (a function) for the next element (as opposed to consing to a fully realized list).

And that covers lazy seqs! Now you know everything there is to know about the sequence abstraction, and we can turn to the collection abstraction!

The Collection Abstraction

The collection abstraction is closely related to the sequence abstraction. All of Clojure’s core data structures—vectors, maps, lists, and sets—take part in both abstractions.

The sequence abstraction is about operating on members individually, whereas the collection abstraction is about the data structure as a whole. For example, the collection functions count, empty?, and every? aren’t about any individual element; they’re about the whole:

(empty? [])
; => true

(empty? ["no!"])
; => false

Practically speaking, you’ll rarely consciously say, “Okay, self! You’re working with the collection as a whole now. Think in terms of the collection abstraction!” Nevertheless, it’s useful to know these concepts that underlie the functions and data structures you’re using.

Now we’ll examine two common collection functions—into and conj—whose similarities can be a bit confusing.

into

One of the most important collection functions is into. As you now know, many seq functions return a seq rather than the original data structure. You’ll probably want to convert the return value back into the original value, and into lets you do that:

(map identity {:sunlight-reaction "Glitter!"})
; => ([:sunlight-reaction "Glitter!"])

(into {} (map identity {:sunlight-reaction "Glitter!"}))
; => {:sunlight-reaction "Glitter!"}

Here, the map function returns a sequential data structure after being given a map data structure, and into converts the seq back into a map.

This will work with other data structures as well:

(map identity [:garlic :sesame-oil :fried-eggs])
; => (:garlic :sesame-oil :fried-eggs)

(into [] (map identity [:garlic :sesame-oil :fried-eggs]))
; => [:garlic :sesame-oil :fried-eggs]

Here, in the first line, map returns a seq, and we use into in the second line to convert the result back to a vector.

In the following example, we start with a vector with two identical entries, map converts it to a list, and then we use into to stick the values into a set.

(map identity [:garlic-clove :garlic-clove])
; => (:garlic-clove :garlic-clove)

(into #{} (map identity [:garlic-clove :garlic-clove]))
; => #{:garlic-clove}

Because sets only contain unique values, the set ends up with just one value in it.

The first argument of into doesn’t have to be empty. Here, the first example shows how you can use into to add elements to a map, and the second shows how you can add elements to a vector.

(into {:favorite-emotion "gloomy"} [[:sunlight-reaction "Glitter!"]])
; => {:favorite-emotion "gloomy" :sunlight-reaction "Glitter!"}

(into ["cherry"] '("pine" "spruce"))
; => ["cherry" "pine" "spruce"]

And, of course, both arguments can be the same type. In this next example, both arguments are maps, whereas all the previous examples had arguments of different types. It works as you’d expect, returning a new map with the elements of the second map added to the first:

(into {:favorite-animal "kitty"} {:least-favorite-smell "dog"
                                  :relationship-with-teenager "creepy"})
; => {:favorite-animal "kitty"
      :relationship-with-teenager "creepy"
      :least-favorite-smell "dog"}

If into were asked to describe its strengths at a job interview, it would say, “I’m great at taking two collections and adding all the elements from the second to the first.”

conj

conj also adds elements to a collection, but it does it in a slightly different way:

(conj [0] [1])
; => [0 [1]]

Whoopsie! Looks like it added the entire vector [1] to [0]. Compare this with into:

(into [0] [1])
; => [0 1]

Here’s how we’d do the same with conj:

(conj [0] 1)
; => [0 1]

Notice that the number 1 is passed as a scalar (singular, non-collection) value, whereas into’s second argument must be a collection.

You can supply as many elements to add with conj as you want, and you can also add to other collections like maps:

(conj [0] 1 2 3 4)
; => [0 1 2 3 4]

(conj {:time "midnight"} [:place "ye olde cemetarium"])
; => {:place "ye olde cemetarium" :time "midnight"}

conj and into are so similar that you could even define conj in terms of into:

(defn my-conj
  [target & additions]
  (into target additions))

(my-conj [0] 1 2 3)
; => [0 1 2 3]

This kind of pattern isn’t that uncommon. You’ll often see two functions that do the same thing, except one takes a rest parameter (conj) and one takes a seqable data structure (into).

Function Functions

Learning to take advantage of Clojure’s ability to accept functions as arguments and return functions as values is really fun, even if it takes some getting used to.

Two of Clojure’s functions, apply and partial, might seem especially weird because they both accept and return functions. Let’s unweird them.

apply

apply explodes a seqable data structure so it can be passed to a function that expects a rest parameter. For example, max takes any number of arguments and returns the greatest of all the arguments. Here’s how you’d find the greatest number:

(max 0 1 2)
; => 2

But what if you want to find the greatest element of a vector? You can’t just pass the vector to max:

(max [0 1 2])
; => [0 1 2]

This doesn’t return the greatest element in the vector because max returns the greatest of all the arguments passed to it, and in this case you’re only passing it a vector containing all the numbers you want to compare, rather than passing in the numbers as separate arguments. apply is perfect for this situation:

(apply max [0 1 2])
; => 2

By using apply, it’s as if you called (max 0 1 2). You’ll often use apply like this, exploding the elements of a collection so that they get passed to a function as separate arguments.

Remember how we defined conj in terms of into earlier? Well, we can also define into in terms of conj by using apply:

(defn my-into
  [target additions]
  (apply conj target additions))

(my-into [0] [1 2 3])
; => [0 1 2 3]

This call to my-into is equivalent to calling (conj [0] 1 2 3).

partial

partial takes a function and any number of arguments. It then returns a new function. When you call the returned function, it calls the original function with the original arguments you supplied it along with the new arguments.

Here’s an example:

(def add10 (partial + 10))
(add10 3) 
; => 13
(add10 5) 
; => 15

(def add-missing-elements
  (partial conj ["water" "earth" "air"]))

(add-missing-elements "unobtainium" "adamantium")
; => ["water" "earth" "air" "unobtainium" "adamantium"]

So when you call add10, it calls the original function and arguments (+ 10) and tacks on whichever arguments you call add10 with. To help clarify how partial works, here’s how you might define it:

(defn my-partial
  [partialized-fn & args]
  (fn [& more-args]
    (apply partialized-fn (into args more-args))))

(def add20 (my-partial + 20))
(add20 3) 
; => 23

In this example, the value of add20 is the anonymous function returned by my-partial. The anonymous function is defined like this:

(fn [& more-args]
  (apply + (into [20] more-args)))

In general, you want to use partials when you find you’re repeating the same combination of function and arguments in many different contexts. This toy example shows how you could use partial to specialize a logger, creating a warn function:

(defn lousy-logger
  [log-level message]
  (condp = log-level
    :warn (clojure.string/lower-case message)
    :emergency (clojure.string/upper-case message)))

(def warn (partial lousy-logger :warn))

(warn "Red light ahead")
; => "red light ahead"

Calling (warn "Red light ahead") here is identical to calling (lousy-logger :warn "Red light ahead").

complement

Earlier you created the identify-vampire function to find one vampire amid a million people. What if you wanted to create a function to find all humans? Perhaps you want to send them thank-you cards for not being an undead predator. Here’s how you could do it:

(defn identify-humans
  [social-security-numbers]
  (filter #(not (vampire? %))
          (map vampire-related-details social-security-numbers)))

Look at the first argument to filter, #(not (vampire? %)). It’s so common to want the complement (the negation) of a Boolean function that there’s a function, complement, for that:

(def not-vampire? (complement vampire?))
(defn identify-humans
  [social-security-numbers]
  (filter not-vampire?
          (map vampire-related-details social-security-numbers)))

Here’s how you might implement complement:

(defn my-complement
  [fun]
  (fn [& args]
    (not (apply fun args))))

(def my-pos? (complement neg?))
(my-pos? 1)  
; => true

(my-pos? -1) 
; => false

As you can see, complement is a humble function. It does one little thing and does it well. complement made it trivial to create a not-vampire? function, and anyone reading the code could understand the code’s intention.

This won’t MapReduce terabytes of data for you or anything like that, but it does demonstrate the power of higher-order functions. They allow you to build up libraries of utility functions in a way that is impossible in some languages. In aggregate, these utility functions make your life a lot easier.

A Vampire Data Analysis Program for the FWPD

To pull everything together, let’s write the beginnings of a sophisticated vampire data analysis program for the Forks, Washington Police Department (FWPD).

The FWPD has a fancy new database technology called CSV (comma-separated values). Your job is to parse this state-of-the-art CSV and analyze it for potential vampires. We’ll do that by filtering on each suspect’s glitter index, a 0–10 prediction of the suspect’s vampireness developed by some teenage girl. Go ahead and create a new Leiningen project for your tool:

lein new app fwpd

Under the new fwpd directory, create a file named suspects.csv and enter contents like the following:

Edward Cullen,10
Bella Swan,0
Charlie Swan,0
Jacob Black,3
Carlisle Cullen,6

Now it’s time to get your hands dirty by building up the fwpd/src/fwpd/core.clj file. I recommend that you start a new REPL session so you can try things out as you go along. In Emacs you can do this by opening fwpd/src/fwpd/core.clj and running M-x cider-restart. Once the REPL is started, delete the contents of core.clj, and then add this:

(ns fwpd.core)
(def filename "suspects.csv")

The first line establishes the namespace, and the second just makes it a tiny bit easier to refer to the CSV you created. You can do a quick sanity check in your REPL by compiling your file (C-c C-k in Emacs) and running this:

(slurp filename)
; => "Edward Cullen,10\nBella Swan,0\nCharlie Swan,0\nJacob Black,3\nCarlisle Cullen,6"

If the slurp function doesn’t return the preceding string, try restarting your REPL session with core.clj open.

Next, add this to core.clj:

➊ (def vamp-keys [:name :glitter-index])

➋ (defn str->int
  [str]
  (Integer. str))

➌ (def conversions {:name identity
                  :glitter-index str->int})

➍ (defn convert
  [vamp-key value]
  ((get conversions vamp-key) value))

Ultimately, you’ll end up with a sequence of maps that look like {:name "Edward Cullen" :glitter-index 10}, and the preceding definitions help you get there. First, vamp-keys ➊ is a vector of the keys that you’ll soon use to create vampire maps. Next, the function str->int ➋ converts a string to an integer. The map conversions ➌ associates a conversion function with each of the vamp keys. You don’t need to transform the name at all, so its conversion function is identity, which just returns the argument passed to it. The glitter index is converted to an integer, so its conversion function is str->int. Finally, the convert function ➍ takes a vamp key and a value, and returns the converted value. Here’s an example:

(convert :glitter-index "3")
; => 3

Now add this to your file:

(defn parse
  "Convert a CSV into rows of columns"
  [string]
  (map #(clojure.string/split % #",")
       (clojure.string/split string #"\n")))

The parse function takes a string and first splits it on the newline character to create a seq of strings. Next, it maps over the seq of strings, splitting each one on the comma character. Try running parse on your CSV:

(parse (slurp filename))
; => (["Edward Cullen" "10"] ["Bella Swan" "0"] ["Charlie Swan" "0"]
      ["Jacob Black" "3"] ["Carlisle Cullen" "6"])

The next bit of code takes the seq of vectors and combines it with your vamp keys to create maps:

(defn mapify
  "Return a seq of maps like {:name \"Edward Cullen\" :glitter-index 10}"
  [rows]
  (map (fn [unmapped-row]
         (reduce (fn [row-map [vamp-key value]]
                   (assoc row-map vamp-key (convert vamp-key value)))
                 {}
                 (map vector vamp-keys unmapped-row)))
       rows))

In this function, map transforms each row—vectors like ["Bella Swan" 0]—into a map by using reduce in a manner similar to the first example in “reduce” above. First, map creates a seq of key-value pairs like ([:name "Bella Swan"] [:glitter-index 0]). Then, reduce builds up a map by associating a vamp key with a converted vamp value into row-map. Here’s the first row mapified:

(first (mapify (parse (slurp filename))))
; => {:glitter-index 10, :name "Edward Cullen"}

Finally, add this glitter-filter function:

(defn glitter-filter
  [minimum-glitter records]
  (filter #(>= (:glitter-index %) minimum-glitter) records))

This takes fully mapified vampire records and filters out those with a :glitter-index less than the provided minimum-glitter:

(glitter-filter 3 (mapify (parse (slurp filename))))
({:name "Edward Cullen", :glitter-index 10}
 {:name "Jacob Black", :glitter-index 3}
 {:name "Carlisle Cullen", :glitter-index 6})

Et voilà! You are now one step closer to fulfilling your dream of being a supernatural-creature-hunting vigilante. You better go round up those sketchy characters!

Summary

In this chapter, you learned that Clojure emphasizes programming to abstractions. The sequence abstraction deals with operating on the individual elements of a sequence, and seq functions often convert their arguments to a seq and return a lazy seq. Lazy evaluation improves performance by delaying computations until they’re needed. The other abstraction you learned about, the collection abstraction, deals with data structures as a whole. Finally, the most important thing you learned is that you should never trust someone who sparkles in sunlight.

Exercises

The vampire analysis program you now have is already decades ahead of anything else on the market. But how could you make it better? I suggest trying the following:

1. Turn the result of your glitter filter into a list of names.
2. Write a function, append, which will append a new suspect to your list of suspects.
3. Write a function, validate, which will check that :name and :glitter-index are present when you append. The validate function should accept two arguments: a map of keywords to validating functions, similar to conversions, and the record to be validated.
4. Write a function that will take your list of maps and convert it back to a CSV string. You’ll need to use the clojure.string/join function.

Good luck, McFishwich!