Functional Programming

So far, you’ve focused on becoming familiar with the tools that Clojure provides: immutable data structures, functions, abstractions, and so on. In this chapter, you’ll learn how to think about your programming tasks in a way that makes the best use of those tools. You’ll begin integrating your experience into a new functional programming mindset.

The core concepts you’ll learn include: what pure functions are and why they’re useful; how to work with immutable data structures and why they’re superior to their mutable cousins; how disentangling data and functions gives you more power and flexibility; and why it’s powerful to program to a small set of data abstractions. Once you shove all this knowledge into your brain matter, you’ll have an entirely new approach to problem solving!

After going over these topics, you’ll put everything you’ve learned to use by writing a terminal-based game inspired by an ancient, mystic mind-training device found in Cracker Barrel restaurants across America: Peg Thing!

Pure Functions: What and Why

Except for println and rand, all the functions you’ve used up till now have been pure functions. What makes them pure functions, and why does it matter? A function is pure if it meets two qualifications:

• It always returns the same result if given the same arguments. This is called referential transparency, and you can add it to your list of $5 programming terms.
• It can’t cause any side effects. That is, the function can’t make any changes that are observable outside the function itself—for example, by changing an externally accessible mutable object or writing to a file.

These qualities make it easier for you to reason about your programs because the functions are completely isolated, unable to impact other parts of your system. When you use them, you don’t have to ask yourself, “What could I break by calling this function?” They’re also consistent: you’ll never need to figure out why passing a function the same arguments results in different return values, because that will never happen.

Pure functions are as stable and problem free as arithmetic (when was the last time you fretted over adding two numbers?). They’re stupendous little bricks of functionality that you can confidently use as the foundation of your program. Let’s look at referential transparency and lack of side effects in more detail to see exactly what they are and how they’re helpful.

Pure Functions Are Referentially Transparent

To return the same result when called with the same argument, pure functions rely only on 1) their own arguments and 2) immutable values to determine their return value. Mathematical functions, for example, are referentially transparent:

(+ 1 2)
; => 3

If a function relies on an immutable value, it’s referentially transparent. The string ", Daniel-san" is immutable, so the following function is also referentially transparent:

(defn wisdom
  [words]
  (str words ", Daniel-san"))

(wisdom "Always bathe on Fridays")
; => "Always bathe on Fridays, Daniel-san"

By contrast, the following functions do not yield the same result with the same arguments; therefore, they are not referentially transparent. Any function that relies on a random number generator cannot be referentially transparent:

(defn year-end-evaluation
  []
  (if (> (rand) 0.5)
    "You get a raise!"
    "Better luck next year!"))

If your function reads from a file, it’s not referentially transparent because the file’s contents can change. The following function, analyze-file, is not referentially transparent, but the function analysis is:

(defn analyze-file
  [filename]
  (analysis (slurp filename)))

(defn analysis
  [text]
  (str "Character count: " (count text)))

When using a referentially transparent function, you never have to consider what possible external conditions could affect the return value of the function. This is especially important if your function is used multiple places or if it’s nested deeply in a chain of function calls. In both cases, you can rest easy knowing that changes to external conditions won’t cause your code to break.

Another way to think about this is that reality is largely referentially transparent. If you think of gravity as a function, then gravitational force is the return value of calling that function on two objects. Therefore, the next time you’re in a programming interview, you can demonstrate your functional programming knowledge by knocking everything off your interviewer’s desk. (This also demonstrates that you know how to apply a function over a collection.)

Pure Functions Have No Side Effects

To perform a side effect is to change the association between a name and its value within a given scope. Here is an example in JavaScript:

var haplessObject = {
  emotion: "Carefree!"
};

var evilMutator = function(object){
  object.emotion = "So emo :'(";
}

evilMutator(haplessObject);
haplessObject.emotion;
// => "So emo :'("

Of course, your program has to have some side effects. It writes to a disk, which changes the association between a filename and a collection of disk sectors; it changes the RGB values of your monitor’s pixels; and so on. Otherwise, there’d be no point in running it.

Side effects are potentially harmful, however, because they introduce uncertainty about what the names in your code are referring to. This leads to situations where it’s very difficult to trace why and how a name came to be associated with a value, which makes it hard to debug the program. When you call a function that doesn’t have side effects, you only have to consider the relationship between the input and the output. You don’t have to worry about other changes that could be rippling through your system.

Functions with side effects, on the other hand, place more of a burden on your mind grapes: now you have to worry about how the world is affected when you call the function. Not only that, but every function that depends on a side-effecting function gets infected by this worry; it, too, becomes another component that requires extra care and thought as you build your program.

If you have any significant experience with a language like Ruby or JavaScript, you’ve probably run into this problem. As an object gets passed around, its attributes somehow change, and you can’t figure out why. Then you have to buy a new computer because you’ve chucked yours out the window. If you’ve read anything about object-oriented design, you know that a lot of writing has been devoted to strategies for managing state and reducing side effects for just this reason.

For all these reasons, it’s a good idea to look for ways to limit the use of side effects in your code. Lucky for you, Clojure makes your job easier by going to great lengths to limit side effects—all of its core data structures are immutable. You cannot change them in place, no matter how hard you try! However, if you’re unfamiliar with immutable data structures, you might feel like your favorite tool has been taken from you. How can you do anything without side effects? Well, that’s what the next section is all about! How about that segue, eh? Eh?

Living with Immutable Data Structures

Immutable data structures ensure that your code won’t have side effects. As you now know with all your heart, this is a good thing. But how do you get anything done without side effects?

Recursion Instead of for/while

Raise your hand if you’ve ever written something like this in JavaScript:

var wrestlers = getAlligatorWrestlers();
var totalBites = 0;
var l = wrestlers.length;

for(var i=0; i < l; i++){
  totalBites += wrestlers[i].timesBitten;
}

Or this:

var allPatients = getArkhamPatients();
var analyzedPatients = [];
var l = allPatients.length;

for(var i=0; i < l; i++){
  if(allPatients[i].analyzed){
    analyzedPatients.push(allPatients[i]);
  }
}

Notice that both examples induce side effects on the looping variable i, as well as a variable outside the loop (totalBites in the first example and analyzedPatients in the second). Using side effects this way—mutating internal variables—is pretty much harmless. You’re creating new values, as opposed to changing an object you’ve received from elsewhere in your program.

But Clojure’s core data structures don’t even allow these harmless mutations. So what can you do instead? First, ignore the fact that you could easily use map and reduce to accomplish the preceding work. In these situations—iterating over some collection to build a result—the functional alternative to mutation is recursion.

Let’s look at the first example, building a sum. Clojure has no assignment operator. You can’t associate a new value with a name without creating a new scope:

(def great-baby-name "Rosanthony")
great-baby-name
; => "Rosanthony"

(let [great-baby-name "Bloodthunder"]
  great-baby-name)
; => "Bloodthunder"

great-baby-name
; => "Rosanthony"

In this example, you first bind the name great-baby-name to "Rosanthony" within the global scope. Next, you introduce a new scope with let. Within that scope, you bind great-baby-name to "Bloodthunder". Once Clojure finishes evaluating the let expression, you’re back in the global scope, and great-baby-name evaluates to "Rosanthony" once again.

Clojure lets you work around this apparent limitation with recursion. The following example shows the general approach to recursive problem solving:

(defn sum
➊   ([vals] (sum vals 0)) 
  ([vals accumulating-total]
➋      (if (empty? vals)  
       accumulating-total
       (sum (rest vals) (+ (first vals) accumulating-total)))))

This function takes two arguments, a collection to process (vals) and an accumulator (accumulating-total), and it uses arity overloading (covered in Chapter 3) to provide a default value of 0 for accumulating-total at ➊.

Like all recursive solutions, this function checks the argument it’s processing against a base condition. In this case, we check whether vals is empty at ➋. If it is, we know that we’ve processed all the elements in the collection, so we return accumulating-total.

If vals isn’t empty, it means we’re still working our way through the sequence, so we recursively call sum passing it two arguments: the tail of vals with (rest vals) and the sum of the first element of vals plus the accumulating total with (+ (first vals) accumulating-total). In this way, we build up accumulating-total and at the same time reduce vals until it reaches the base case of an empty collection.

Here’s what the recursive function call might look like if we separate out each time it recurs:

(sum [39 5 1]) ; single-arity body calls two-arity body
(sum [39 5 1] 0)
(sum [5 1] 39)
(sum [1] 44)
(sum [] 45) ; base case is reached, so return accumulating-total
; => 45

Each recursive call to sum creates a new scope where vals and accumulating-total are bound to different values, all without needing to alter the values originally passed to the function or perform any internal mutation. As you can see, you can get along fine without mutation.

Note that you should generally use recur when doing recursion for performance reasons. The reason is that Clojure doesn’t provide tail call optimization, a topic I will never bring up again! (Check out this URL for more information: http://en.wikipedia.org/wiki/Tail_call.) So here’s how you’d do this with recur:

(defn sum
  ([vals]
     (sum vals 0))
  ([vals accumulating-total]
     (if (empty? vals)
       accumulating-total
       (recur (rest vals) (+ (first vals) accumulating-total)))))

Using recur isn’t that important if you’re recursively operating on a small collection, but if your collection contains thousands or millions values, you will definitely need to whip out recur so you don’t blow up your program with a stack overflow.

One last thing! You might be saying, “Wait a minute—what if I end up creating thousands of intermediate values? Doesn’t this cause the program to thrash because of garbage collection or whatever?”

Very good question, eagle-eyed reader! The answer is no! The reason is that, behind the scenes, Clojure’s immutable data structures are implemented using structural sharing, which is totally beyond the scope of this book. It’s kind of like Git! Read this great article if you want to know more: http://hypirion.com/musings/understanding-persistent-vector-pt-1.

Function Composition Instead of Attribute Mutation

Another way you might be used to using mutation is to build up the final state of an object. In the following Ruby example, the GlamourShotCaption object uses mutation to clean input by removing trailing spaces and capitalizing "lol":

class GlamourShotCaption
  attr_reader :text
  def initialize(text)
    @text = text
    clean!
  end

  private
  def clean!
    text.trim!
    text.gsub!(/lol/, "LOL")
  end
end

best = GlamourShotCaption.new("My boa constrictor is so sassy lol!  ")
best.text
; => "My boa constrictor is so sassy LOL!"

In this code, the class GlamourShotCaption encapsulates the knowledge of how to clean a glamour shot caption. On creating a GlamourShotCaption object, you assign text to an instance variable and progressively mutate it.

Listing 5-1 shows how you might do this in Clojure:

(require '[clojure.string :as s])
(defn clean
  [text]
  (s/replace (s/trim text) #"lol" "LOL"))

(clean "My boa constrictor is so sassy lol!  ")
; => "My boa constrictor is so sassy LOL!"

1. 5-1. Using function composition to modify a glamour shot caption

In the first line, we use require to access the string function library (I’ll discuss this function and related concepts in Chapter 6). Otherwise, the code is easy peasy. No mutation required. Instead of progressively mutating an object, the clean function works by passing an immutable value, text, to a pure function, s/trim, which returns an immutable value ("My boa constrictor is so sassy lol!"; the spaces at the end of the string have been trimmed). That value is then passed to the pure function s/replace, which returns another immutable value ("My boa constrictor is so sassy LOL!").

Combining functions like this—so that the return value of one function is passed as an argument to another—is called function composition. In fact, this isn’t so different from the previous example, which used recursion, because recursion continually passes the result of a function to another function; it just happens to be the same function. In general, functional programming encourages you to build more complex functions by combining simpler functions.

This comparison also starts to reveal some limitations of object-oriented programming (OOP). In OOP, one of the main purposes of classes is to protect against unwanted modification of private data—something that isn’t necessary with immutable data structures. You also have to tightly couple methods with classes, thus limiting the reusability of the methods. In the Ruby example, you have to do extra work to reuse the clean! method. In Clojure, clean will work on any string at all. By both a) decoupling functions and data, and b) programming to a small set of abstractions, you end up with more reusable, composable code. You gain power and lose nothing.

Going beyond immediately practical concerns, the differences between the way you write object-oriented and functional code point to a deeper difference between the two mindsets. Programming is about manipulating data for your own nefarious purposes (as much as you can say it’s about anything). In OOP, you think about data as something you can embody in an object, and you poke and prod it until it looks right. During this process, your original data is lost forever unless you’re very careful about preserving it. By contrast, in functional programming you think of data as unchanging, and you derive new data from existing data. During this process, the original data remains safe and sound. In the preceding Clojure example, the original caption doesn’t get modified. It’s safe in the same way that numbers are safe when you add them together; you don’t somehow transform 4 into 7 when you add 3 to it.

Once you are confident using immutable data structures to get stuff done, you’ll feel even more confident because you won’t have to worry about what dirty code might be getting its greasy paws on your precious, mutable variables. It’ll be great!

Cool Things to Do with Pure Functions

You can derive new functions from existing functions in the same way that you derive new data from existing data. You’ve already seen one function, partial, that creates new functions. This section introduces you to two more functions, comp and memoize, which rely on referential transparency, immutability, or both.

comp

It’s always safe to compose pure functions like we just did in the previous section, because you only need to worry about their input/output relationship. Composing functions is so common that Clojure provides a function, comp, for creating a new function from the composition of any number of functions. Here’s a simple example:

((comp inc *) 2 3)
; => 7

Here, you create an anonymous function by composing the inc and * functions. Then, you immediately apply this function to the arguments 2 and 3. The function multiplies the numbers 2 and 3 and then increments the result. Using math notation, you’d say that, in general, using comp on the functions f1, f2, ... fn, creates a new function g such that g(x1, x2, ... xn) equals f1( f2( fn(x1, x2, ... xn))). One detail to note here is that the first function applied—* in the code shown here—can take any number of arguments, whereas the remaining functions must be able to take only one argument.

Here’s an example that shows how you could use comp to retrieve character attributes in role-playing games:

(def character
  {:name "Smooches McCutes"
   :attributes {:intelligence 10
                :strength 4
                :dexterity 5}})
(def c-int (comp :intelligence :attributes))
(def c-str (comp :strength :attributes))
(def c-dex (comp :dexterity :attributes))

(c-int character)
; => 10

(c-str character)
; => 4

(c-dex character)
; => 5

In this example, you created three functions that help you look up a character’s attributes. Instead of using comp, you could just have written something like this for each attribute:

(fn [c] (:strength (:attributes c)))

But comp is more elegant because it uses less code to convey more meaning. When you see comp, you immediately know that the resulting function’s purpose is to combine existing functions in a well-known way.

What do you do if one of the functions you want to compose needs to take more than one argument? You wrap it in an anonymous function. Have a look at this next snippet, which calculates the number of spell slots your character has based on her intelligence attribute:

(defn spell-slots
  [char]
  (int (inc (/ (c-int char) 2))))

(spell-slots character)
; => 6

First, you divide intelligence by two, then you add one, and then you use the int function to round down. Here’s how you could do the same thing with comp:

(def spell-slots-comp (comp int inc #(/ % 2) c-int))

To divide by two, all you needed to do was wrap the division in an anony­mous function.

Clojure’s comp function can compose any number of functions. To get a hint of how it does this, here’s an implementation that composes just two functions:

(defn two-comp
  [f g]
  (fn [& args]
    (f (apply g args))))

I encourage you to evaluate this code and use two-comp to compose two functions! Also, try reimplementing Clojure’s comp function so you can compose any number of functions.

memoize

Another cool thing you can do with pure functions is memoize them so that Clojure remembers the result of a particular function call. You can do this because, as you learned earlier, pure functions are referentially transparent. For example, + is referentially transparent. You can replace

(+ 3 (+ 5 8))

with

(+ 3 13)

or

16

and the program will have the same behavior.

Memoization lets you take advantage of referential transparency by storing the arguments passed to a function and the return value of the function. That way, subsequent calls to the function with the same arguments can return the result immediately. This is especially useful for functions that take a lot of time to run. For example, in this unmemoized function, the result is returned after one second:

(defn sleepy-identity
  "Returns the given value after 1 second"
  [x]
  (Thread/sleep 1000)
  x)
(sleepy-identity "Mr. Fantastico")
; => "Mr. Fantastico" after 1 second

(sleepy-identity "Mr. Fantastico")
; => "Mr. Fantastico" after 1 second

However, if you create a new, memoized version of sleepy-identity with memoize, only the first call waits one second; every subsequent function call returns immediately:

(def memo-sleepy-identity (memoize sleepy-identity))
(memo-sleepy-identity "Mr. Fantastico")
; => "Mr. Fantastico" after 1 second

(memo-sleepy-identity "Mr. Fantastico")
; => "Mr. Fantastico" immediately

Pretty cool! From here on out, memo-sleepy-identity will not incur the initial one-second cost when called with "Mr. Fantastico". This implementation could be useful for functions that are computationally intensive or that make network requests.

Peg Thing

It’s that time! Time to build a terminal implementation of Peg Thing using everything you’ve learned so far: immutable data structures, lazy sequences, pure functions, recursion—everything! Doing this will help you understand how to combine these concepts and techniques to solve larger problems. Most important, you’ll learn how to model the changes that result from each move a player makes without having to mutate objects like you would in OOP.

To build the game, you’ll first learn the game’s mechanics and how to start and play the program. Then, I’ll explain the code’s organization. Finally, I’ll walk through each function.

You can find the complete code repository for Peg Thing at https://www.nostarch.com/clojure/.

Playing

As mentioned earlier, Peg Thing is based on the secret mind-sharpening tool passed down from ye olden days and is now distributed by Cracker Barrel.

If you’re not familiar with the game, here are the mechanics. You start out with a triangular board consisting of holes filled with pegs, and one hole has a missing a peg, as shown in Figure 5-1.

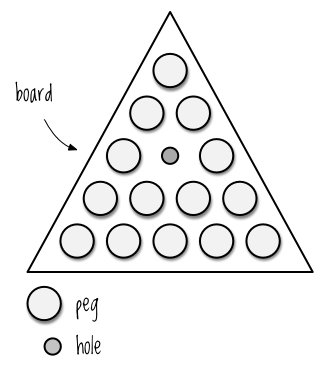
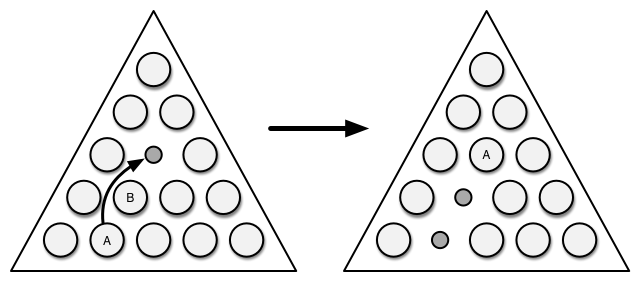
The object of the game is to remove as many pegs as possible. You do this by jumping over pegs. In Figure 5-2, peg A jumps over peg B into the empty hole, and you remove peg B from the board.

To start Peg Thing, download the code, and then run lein run in your terminal while in the pegthing directory. A prompt appears that looks like this:

Get ready to play Peg Thing!
How many rows? [5]

Now you can enter the number of rows the board will have, using 5 as the default. If you want five rows, just press enter (otherwise, type a number and press enter). You’ll then see this:

Here's your board:
       a0
      b0 c0
    d0 e0 f0
   g0 h0 i0 j0
 k0 l0 m0 n0 o0
Remove which peg? [e]

Each letter identifies a position on the board. The number 0 (which should be blue, but if it’s not, it’s no big deal) indicates that a position is filled. Before gameplay begins, one peg must be empty, so the prompt asks you to enter the position of the first to peg to remove. The default is the center peg, e, but you can choose a different one. After you remove the peg, you’ll see this:

Here's your board:
       a0
      b0 c0
    d0 e- f0
   g0 h0 i0 j0
 k0 l0 m0 n0 o0
Move from where to where? Enter two letters:

Notice that the e position now has a dash, - (which should be red, but if it’s not, it’s no big deal). The dash indicates that the position is empty. To move, you enter the position of the peg you want to pick up followed by the position of the empty position that you want to place it in. If you enter le, for example, you’ll get this:

Here's your board:
       a0
      b0 c0
    d0 e0 f0
   g0 h- i0 j0
 k0 l- m0 n0 o0
Move from where to where? Enter two letters:

You’ve moved the peg from l to e, jumping over h and removing its peg according to the rule shown in Figure 5-2. The game continues to prompt you for moves until no moves are available, whereupon it prompts you to play again.

Code Organization

The program has to handle four major tasks, and the source code is organized accordingly, with the functions for each of these tasks grouped together:

1. Creating a new board
2. Returning a board with the result of the player’s move
3. Representing a board textually
4. Handling user interaction

Two more points about the organization: First, the code has a basic architecture, or conceptual organization, of two layers. The top layer consists of the functions for handling user interaction. These functions produce all of the program’s side effects, printing out the board and presenting prompts for player interaction. The functions in this layer use the functions in the bottom layer to create a new board, make moves, and create a textual representation, but the functions in the bottom layer don’t use those in the top layer at all. Even for a program this small, a little architecture helps make the code more manageable.

Second, I’ve tried as much as possible to decompose tasks into small functions so that each does one tiny, understandable task. Some of these functions are used by only one other function. I find this helpful because it lets me name each tiny subtask, allowing me to better express the intention of the code.

But before all the architecture, there’s this:

(ns pegthing.core
  (require [clojure.set :as set])
  (:gen-class))

(declare successful-move prompt-move game-over query-rows)

I’ll explain the functions here in more detail in Chapter 6. If you’re curious about what’s going on, the short explanation is that (require [clojure.set :as set]) allows you to easily use functions in the clojure.set namespace, (:gen-class) allows you to run the program from the command line, and (declare successful-move prompt-move game-over query-rows) allows functions to refer to those names before they’re defined. If that doesn’t quite make sense yet, trust that I will explain it soon.

Creating the Board

The data structure you use to represent the board should make it easy for you to print the board, check whether a player has made a valid move, actually perform a move, and check whether the game is over. You could structure the board in many ways to allow these tasks. In this case, you’ll represent the board using a map with numerical keys corresponding to each board position and values containing information about that position’s connections. The map will also contain a :rows key, storing the total number of rows. Figure 5-3 shows a board with each position numbered.

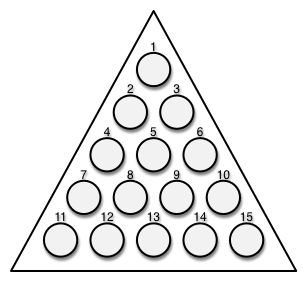
Here’s the data structure built to represent it:

{1  {:pegged true, :connections {6 3, 4 2}},
 2  {:pegged true, :connections {9 5, 7 4}},
 3  {:pegged true, :connections {10 6, 8 5}},
 4  {:pegged true, :connections {13 8, 11 7, 6 5, 1 2}},
 5  {:pegged true, :connections {14 9, 12 8}},
 6  {:pegged true, :connections {15 10, 13 9, 4 5, 1 3}},
 7  {:pegged true, :connections {9 8, 2 4}},
 8  {:pegged true, :connections {10 9, 3 5}},
 9  {:pegged true, :connections {7 8, 2 5}},
 10 {:pegged true, :connections {8 9, 3 6}},
 11 {:pegged true, :connections {13 12, 4 7}},
 12 {:pegged true, :connections {14 13, 5 8}},
 13 {:pegged true, :connections {15 14, 11 12, 6 9, 4 8}},
 14 {:pegged true, :connections {12 13, 5 9}},
 15 {:pegged true, :connections {13 14, 6 10}},
 :rows 5}

You might be wondering why, when you play the game, each position is represented by a letter but here the positions are represented by numbers. Using numbers for the internal representation allows you to take advantage of some mathematical properties of the board layout when validating and making moves. Letters, on the other hand, are better for display because they take up only one character space. Some conversion functions are covered in “Rendering and Printing the Board” on page 120.

In the data structure, each position is associated with a map that reads something like this:

{:pegged true, :connections {6 3, 4 2}}

The meaning of :pegged is clear; it represents whether that position has a peg in it. :connections is a bit more cryptic. It’s a map where each key identifies a legal destination, and each value represents the position that would be jumped over. So pegs in position 1, for example, can jump to position 6 over position 3. This might seem backward, but you’ll learn the rationale for it later when you see how move validation is implemented.

Now that you’ve seen what the final map representing the board should look like, we can start exploring the functions that actually build up this map in the program. You won’t simply start assigning mutable states willy-nilly to represent each position and whether it’s pegged or not. Instead, you’ll use nested recursive function calls to build up the final board position by position. It’s analogous to the way you created the glamour shot caption earlier, deriving new data from input by passing an argument through a chain of functions to get your final result.

The first few expressions in this section of the code deal with triangular numbers. Triangular numbers are generated by adding the first n natural numbers. The first triangular number is 1, the second is 3 (1 + 2), the third is 6 (1 + 2 + 3), and so on. These numbers line up nicely with the position numbers at the end of every row on the board, which will turn out to be a very useful property. First, you define the function tri*, which can create a lazy sequence of triangular numbers:

(defn tri*
  "Generates lazy sequence of triangular numbers"
  ([] (tri* 0 1))
  ([sum n]
     (let [new-sum (+ sum n)]
       (cons new-sum (lazy-seq (tri* new-sum (inc n)))))))

To quickly recap how this works, calling tri* with no arguments will recursively call (tri* 0 1). This returns a lazy list whose element is new-sum, which in this case evaluates to 1. The lazy list includes a recipe for generating the next element of the list when it’s requested, as described in Chapter 4.

The next expression calls tri*, actually creating the lazy sequence and binding it to tri:

(def tri (tri*))

You can verify that it actually works:

(take 5 tri)
; => (1 3 6 10 15)

And the next few functions operate on the sequence of triangular numbers. triangular? figures out if its argument is in the tri lazy sequence. It works by using take-while to create a sequence of triangular numbers whose last element is a triangular number that’s less than or equal to the argument. Then it compares the last element to the argument:

(defn triangular?
  "Is the number triangular? e.g. 1, 3, 6, 10, 15, etc"
  [n]
  (= n (last (take-while #(>= n %) tri))))
(triangular? 5) 
; => false

(triangular? 6) 
; => true

Next, there’s row-tri, which takes a row number and gives you the triangular number at the end of that row:

(defn row-tri
  "The triangular number at the end of row n"
  [n]
  (last (take n tri)))
(row-tri 1) 
; => 1

(row-tri 2) 
; => 3

(row-tri 3) 
; => 6

Lastly, there’s row-num, which takes a board position and returns the row that it belongs to:

(defn row-num
  "Returns row number the position belongs to: pos 1 in row 1,
  positions 2 and 3 in row 2, etc"
  [pos]
  (inc (count (take-while #(> pos %) tri))))
(row-num 1) 
; => 1
(row-num 5) 
; => 3

After that comes connect, which is used to actually form a mutual connection between two positions:

(defn connect
  "Form a mutual connection between two positions"
  [board max-pos pos neighbor destination]
  (if (<= destination max-pos)
    (reduce (fn [new-board [p1 p2]]
              (assoc-in new-board [p1 :connections p2] neighbor))
            board
            [[pos destination] [destination pos]])
    board))

(connect {} 15 1 2 4)
; => {1 {:connections {4 2}}
      4 {:connections {1 2}}}

The first thing connect does is check whether the destination is actually a position on the board by confirming that it’s less than the board’s max position. For example, if you have five rows, the max position is 15. However, when the game board is created, the connect function will be called with arguments like (connect {} 15 7 16 22). The if statement at the beginning of connect makes sure your program doesn’t allow such outrageous connections, and simply returns the unmodified board when you ask it to do something silly.

Next, connect uses recursion through reduce to progressively build up the final state of the board. In this example, you’re reducing over the nested vectors [[1 4] [4 1]]. This is what allows you to return an updated board with both pos and destination (1 and 4) pointing to each other in their connections.

The anonymous function passed to reduce uses a function, assoc-in, which you haven’t seen before. Whereas the function get-in lets you look up values in nested maps, assoc-in lets you return a new map with the given value at the specified nesting. Here are a couple of examples:

(assoc-in {} [:cookie :monster :vocals] "Finntroll")
; => {:cookie {:monster {:vocals "Finntroll"}}}

(get-in {:cookie {:monster {:vocals "Finntroll"}}} [:cookie :monster])
; => {:vocals "Finntroll"}

(assoc-in {} [1 :connections 4] 2)
; => {1 {:connections {4 2}}}

In these examples, you can see that new, nested maps are created to accommodate all the keys provided.

Now we have a way to connect two positions, but how should the program choose two positions to connect in the first place? That’s handled by connect-right, connect-down-left, and connect-down-right:

(defn connect-right
  [board max-pos pos]
  (let [neighbor (inc pos)
        destination (inc neighbor)]
    (if-not (or (triangular? neighbor) (triangular? pos))
      (connect board max-pos pos neighbor destination)
      board)))

(defn connect-down-left
  [board max-pos pos]
  (let [row (row-num pos)
        neighbor (+ row pos)
        destination (+ 1 row neighbor)]
    (connect board max-pos pos neighbor destination)))

(defn connect-down-right
  [board max-pos pos]
  (let [row (row-num pos)
        neighbor (+ 1 row pos)
        destination (+ 2 row neighbor)]
    (connect board max-pos pos neighbor destination)))

These functions each take the board’s max position and a board position and use a little triangle math to figure out which numbers to feed to connect. For example, connect-down-left will attempt to connect position 1 to position 4. In case you’re wondering why the functions connect-left, connect-up-left, and connect-up-right aren’t defined, the reason is that the existing functions actually cover these cases. connect returns a board with the mutual connection established; when 4 connects right to 6, 6 connects left to 4. Here are a couple of examples:

(connect-down-left {} 15 1)
; => {1 {:connections {4 2}
      4 {:connections {1 2}}}}

(connect-down-right {} 15 3)
; => {3  {:connections {10 6}}
      10 {:connections {3 6}}}

In the first example, connect-down-left takes an empty board with a max position of 15 and returns a new board populated with the mutual connection between the 1 position and the position below and to the left of it. connect-down-right does something similar, returning a board populated with the mutual connection between 3 and the position below it and to its right.

The next function, add-pos, is interesting because it actually reduces on a vector of functions, applying each in turn to build up the resulting board. But first it updates the board to indicate that a peg is in the given position:

(defn add-pos
  "Pegs the position and performs connections"
  [board max-pos pos]
  (let [pegged-board (assoc-in board [pos :pegged] true)]
    (reduce (fn [new-board connection-creation-fn]
              (connection-creation-fn new-board max-pos pos))
            pegged-board
            [connect-right connect-down-left connect-down-right])))

(add-pos {} 15 1)
{1 {:connections {6 3, 4 2}, :pegged true}
 4 {:connections {1 2}}
 6 {:connections {1 3}}}

It’s like this function is first saying, in the pegged-board binding, “Add a peg to the board at position X.” Then, in reduce, it says, “Take the board with its new peg at position X, and try to connect position X to a legal, rightward position. Take the board that results from that operation, and try to connect position X to a legal, down-left position. Finally, take the board that results from that operation, and try to connect position X to a legal, down-right position. Return the resulting board.”

Reducing over functions like this is another way of composing functions. To illustrate, here’s another way of defining the clean function in Listing 5-1 (page 103):

(defn clean
  [text]
  (reduce (fn [string string-fn] (string-fn string))
          text
          [s/trim #(s/replace % #"lol" "LOL")]))

This redefinition of clean reduces a vector of functions by applying the first function, s/trim, to an initial string, then applying the next function, the anonymous function #(s/replace % #"lol" "LOL"), to the result.

Reducing over a collection of functions is not a technique you’ll use often, but it’s occasionally useful, and it demonstrates the versatility of functional programming.

Last among our board creation functions is new-board:

(defn new-board
  "Creates a new board with the given number of rows"
  [rows]
  (let [initial-board {:rows rows}
        max-pos (row-tri rows)]
    (reduce (fn [board pos] (add-pos board max-pos pos))
            initial-board
            (range 1 (inc max-pos)))))

The code first creates the initial, empty board and gets the max position. Assuming that you’re using five rows, the max position will be 15. Next, the function uses (range 1 (inc max-pos)) to get a list of numbers from 1 to 15, other­wise known as the board’s positions. Finally, it reduces over the list of positions. Each iteration of the reduction calls (add-pos board max-pos pos), which, as you saw earlier, takes an existing board and returns a new one with the position added.

Moving Pegs

The next section of code validates and performs peg moves. Many of the functions (pegged?, remove-peg, place-peg, move-peg) are simple, self-explanatory one-liners:

(defn pegged?
  "Does the position have a peg in it?"
  [board pos]
  (get-in board [pos :pegged]))

(defn remove-peg
  "Take the peg at given position out of the board"
  [board pos]
  (assoc-in board [pos :pegged] false))

(defn place-peg
  "Put a peg in the board at given position"
  [board pos]
  (assoc-in board [pos :pegged] true))

(defn move-peg
  "Take peg out of p1 and place it in p2"
  [board p1 p2]
  (place-peg (remove-peg board p1) p2))

Let’s take a moment to appreciate how neat this code is. This is where you would usually perform mutation in an object-oriented program; after all, how else would you change the board? However, these are all pure functions, and they do the job admirably. I also like that you don’t need the overhead of classes to use these little guys. It feels somehow lighter to program like this.

Next up is valid-moves:

(defn valid-moves
  "Return a map of all valid moves for pos, where the key is the
  destination and the value is the jumped position"
  [board pos]
  (into {}
        (filter (fn [[destination jumped]]
                  (and (not (pegged? board destination))
                       (pegged? board jumped)))
                (get-in board [pos :connections]))))

This code goes through each of the given position’s connections and tests whether the destination position is empty and the jumped position has a peg. To see this in action, you can create a board with the 4 position empty:

(def my-board (assoc-in (new-board 5) [4 :pegged] false))

Figure 5-4 shows what that board would look like.

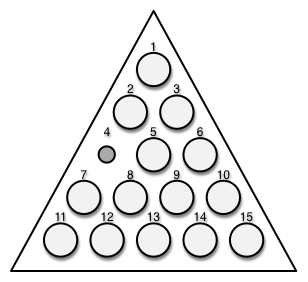
Given this board, positions 1, 6, 11, and 13 have valid moves, but all others don’t:

(valid-moves my-board 1)  ; => {4 2}
(valid-moves my-board 6)  ; => {4 5}
(valid-moves my-board 11) ; => {4 7}
(valid-moves my-board 5)  ; => {}
(valid-moves my-board 8)  ; => {}

You might be wondering why valid-moves returns a map instead of, say, a set or vector. The reason is that returning a map allows you to easily look up a destination position to check whether a specific move is valid, which is what valid-move? (the next function) does:

(defn valid-move?
  "Return jumped position if the move from p1 to p2 is valid, nil
  otherwise"
  [board p1 p2]
  (get (valid-moves board p1) p2))
  
(valid-move? my-board 8 4) ; => nil
(valid-move? my-board 1 4) ; => 2

Notice that valid-move? looks up the destination position from the map and then returns the position of the peg that would be jumped over. This is another nice benefit of having valid-moves return a map, because the jumped position retrieved from the map is exactly what we want to pass on to the next function, make-move. When you take the time to construct a rich data structure, it’s easier to perform useful operations.

(defn make-move
  "Move peg from p1 to p2, removing jumped peg"
  [board p1 p2]
  (if-let [jumped (valid-move? board p1 p2)]
    (move-peg (remove-peg board jumped) p1 p2)))

if-let is a nifty way to say, “If an expression evaluates to a truthy value, then bind that value to a name the same way that I can in a let expression. Otherwise, if I’ve provided an else clause, perform that else clause; if I haven’t provided an else clause, return nil.” In this case, the test expression is (valid-move? board p1 p2), and you’re assigning the result to the name jumped if the result is truthy. That’s used in the call to move-peg, which returns a new board. You don’t supply an else clause, so if the move isn’t valid, the return value of the whole expression is nil.

Finally, the function can-move? is used to determine whether the game is over by finding the first pegged positions with moves available:

(defn can-move?
  "Do any of the pegged positions have valid moves?"
  [board]
  (some (comp not-empty (partial valid-moves board))
        (map first (filter #(get (second %) :pegged) board))))

The question mark at the end of this function name indicates it’s a predicate function, a function that’s meant to be used in Boolean expressions. Predicate is taken from predicate logic, which concerns itself with determining whether a statement is true or false. (You’ve already seen some built-in predicate functions, like empty? and every?.)

can-move? works by getting a sequence of all pegged positions with (map first (filter #(get (second %) :pegged) board)). You can break this down further into the filter and map function calls: because filter is a seq function, it converts board, a map, into a seq of two-element vectors (also called tuples), which looks something like this:

([1 {:connections {6 3, 4 2}, :pegged true}]
 [2 {:connections {9 5, 7 4}, :pegged true}])

The first element of the tuple is a position number, and the second is that position’s information. filter then applies the anonymous function #(get (second %) :pegged) to each of these tuples, filtering out the tuples where the position’s information indicates that the position is not currently housing a peg. Finally, the result is passed to map, which calls first on each tuple to grab just the position number from the tuples.

After you get a seq of pegged positions numbers, you call a predicate function on each one to find the first position that returns a truthy value. The predicate function is created with (comp not-empty (partial valid-moves board)). The idea is to first return a map of all valid moves for a position and then test whether that map is empty.

First, the expression (partial valid-moves board) derives an anonymous function from valid-moves with the first argument, board, filled in using partial (because you’re using the same board each time you call valid-moves). The new function can take a position and return the map of all its valid moves for the current board.

Second, you use comp to compose this function with not-empty. This function is self-descriptive; it returns true if the given collection is empty and false otherwise.

What’s most interesting about this bit of code is that you’re using a chain of functions to derive a new function, similar to how you use chains of functions to derive new data. In Chapter 3, you learned that Clojure treats functions as data in that functions can receive functions as arguments and return them. Hopefully, this shows why that feature is fun and useful.

Rendering and Printing the Board

The first few expressions in the board representation and printing section just define constants:

(def alpha-start 97)
(def alpha-end 123)
(def letters (map (comp str char) (range alpha-start alpha-end)))
(def pos-chars 3)

The bindings alpha-start and alpha-end set up the beginning and end of the numerical values for the letters a through z. We use those to build up a seq of letters. char, when applied to an integer, returns the character corresponding to that integer, and str turns the char into a string. pos-chars is used by the function row-padding to determine how much spacing to add to the beginning of each row. The next few definitions, ansi-styles, ansi, and colorize output colored text to the terminal.

The functions render-pos, row-positions, row-padding, and render-row create strings to represent the board:

(defn render-pos
  [board pos]
  (str (nth letters (dec pos))
       (if (get-in board [pos :pegged])
         (colorize "0" :blue)
         (colorize "-" :red))))

(defn row-positions
  "Return all positions in the given row"
  [row-num]
  (range (inc (or (row-tri (dec row-num)) 0))
         (inc (row-tri row-num))))

(defn row-padding
  "String of spaces to add to the beginning of a row to center it"
  [row-num rows]
  (let [pad-length (/ (* (- rows row-num) pos-chars) 2)]
    (apply str (take pad-length (repeat " ")))))

(defn render-row
  [board row-num]
  (str (row-padding row-num (:rows board))
       (clojure.string/join " " (map (partial render-pos board) 
                                     (row-positions row-num)))))

If you work from the bottom up, you can see that render-row calls each of the functions above it to return the string representation of the given row. Notice the expression (map (partial render-pos board) (row-positions row-num)). This demonstrates a good use case for partials by applying the same function multiple times with one or more arguments filled in, just like in the can-move? function shown earlier.

Notice too that render-pos uses a letter rather than a number to identify each position. This saves a little space when the board is displayed, because it allows only one character per position to represent a five-row board.

Finally, print-board merely iterates over each row number with doseq, printing the string representation of that row:

(defn print-board
  [board]
  (doseq [row-num (range 1 (inc (:rows board)))]
    (println (render-row board row-num))))

You use doseq when you want to perform side-effecting operations (like printing to a terminal) on the elements of a collection. The vector that immediately follows the name doseq describes how to bind all the elements in a collection to a name one at a time so you can operate on them. In this instance, you’re assigning the numbers 1 through 5 (assuming there are five rows) to the name row-num so you can print each row.

Although printing the board technically falls under interaction, I wanted to show it here with the rendering functions. When I first started writing this game, the print-board function also generated the board’s string representation. However, now print-board defers all rendering to pure functions, which makes the code easier to understand and decreases the surface area of our impure functions.

Player Interaction

The next collection of functions handles player interaction. First, there’s letter->pos, which converts a letter (which is how the positions are displayed and identified by players) to the corresponding position number:

(defn letter->pos
  "Converts a letter string to the corresponding position number"
  [letter]
  (inc (- (int (first letter)) alpha-start)))

Next, the helper function get-input allows you to read and clean the player’s input. You can also provide a default value, which is used if the player presses enter without typing anything:

(defn get-input
  "Waits for user to enter text and hit enter, then cleans the input"
  ([] (get-input nil))
  ([default]
     (let [input (clojure.string/trim (read-line))]
       (if (empty? input)
         default
         (clojure.string/lower-case input)))))

The next function, characters-as-strings, is a tiny helper function used by prompt-move to take in a string and return a collection of letters with all nonalphabetic input discarded:

(characters-as-strings "a   b")
; => ("a" "b")

(characters-as-strings "a   cb")
; => ("a" "c" "b")

Next, prompt-move reads the player’s input and acts on it:

(defn prompt-move
  [board]
  (println "\nHere's your board:")
  (print-board board)
  (println "Move from where to where? Enter two letters:")
  (let [input (map letter->pos (characters-as-strings (get-input)))]
    (if-let [new-board (make-move➊ board (first input) (second input))]
      (user-entered-valid-move new-board)
      (user-entered-invalid-move board))))

At ➊, make-move returns nil if the player’s move was invalid, and you use that information to inform her of her mistake with the user-entered-invalid-move function. You pass the unmodified board to user-entered-invalid-move so that it can prompt the player with the board again. Here’s the function definition:

(defn user-entered-invalid-move
  "Handles the next step after a user has entered an invalid move"
  [board]
  (println "\n!!! That was an invalid move :(\n")
  (prompt-move board))

However, if the move is valid, the new-board is passed off to user-entered-valid-move, which hands control back to prompt-move if there are still moves to be made:

(defn user-entered-valid-move
  "Handles the next step after a user has entered a valid move"
  [board]
  (if (can-move? board)
    (prompt-move board)
    (game-over board)))

In our board creation functions, we saw how recursion was used to build up a value using immutable data structures. The same thing is happening here, only it involves two mutually recursive functions and some user input. No mutable attributes in sight!

What happens when the game is over? This is what happens:

(defn game-over
  "Announce the game is over and prompt to play again"
  [board]
  (let [remaining-pegs (count (filter :pegged (vals board)))]
    (println "Game over! You had" remaining-pegs "pegs left:")
    (print-board board)
    (println "Play again? y/n [y]")
    (let [input (get-input "y")]
      (if (= "y" input)
        (prompt-rows)
        (do
          (println "Bye!")
          (System/exit 0))))))

All that’s going on here is that the game tells you how you did, prints the final board, and prompts you to play again. If you select y, the game calls prompt-rows, which brings us to the final set of functions, those used to start a new game:

(defn prompt-empty-peg
  [board]
  (println "Here's your board:")
  (print-board board)
  (println "Remove which peg? [e]")
  (prompt-move (remove-peg board (letter->pos (get-input "e")))))

(defn prompt-rows
  []
  (println "How many rows? [5]")
  (let [rows (Integer. (get-input 5))
        board (new-board rows)]
    (prompt-empty-peg board)))

You use prompt-rows to start a game, getting the player’s input on how many rows to include. Then you pass control on to prompt-empty-peg so the player can tell the game which peg to remove first. From there, the program prompts you for moves until there aren’t any moves left.

Even though all of this program’s side effects are relatively harmless (all you’re doing is prompting and printing), sequestering them in their own functions like this is a best practice for functional programming. In general, you will reap more benefits from functional programming if you identify the bits of functionality that are referentially transparent and side-effect free, and place those bits in their own functions. These functions are not capable of causing bizarre bugs in unrelated parts of your program. They’re easier to test and develop in the REPL because they rely only on the arguments you pass them, not on some complicated hidden state object.

Summary

Pure functions are referentially transparent and side-effect free, which makes them easy to reason about. To get the most from Clojure, try to keep your impure functions to a minimum. In an immutable world, you use recursion instead of for/while loops, and function composition instead of successions of mutations. Pure functions allow powerful techniques like function composition functions and memoization. They’re also super fun!

Exercises

One of the best ways to develop your functional programming skills is to try to implement existing functions. To that end, most of the following exercises suggest a function for you to implement, but don’t stop there; go through the Clojure cheat sheet (http://clojure.org/cheatsheet/) and pick more!

1. You used (comp :intelligence :attributes) to create a function that returns a character’s intelligence. Create a new function, attr, that you can call like (attr :intelligence) and that does the same thing.
2. Implement the comp function.
3. Implement the assoc-in function. Hint: use the assoc function and define its parameters as [m [k & ks] v].
4. Look up and use the update-in function.
5. Implement update-in.